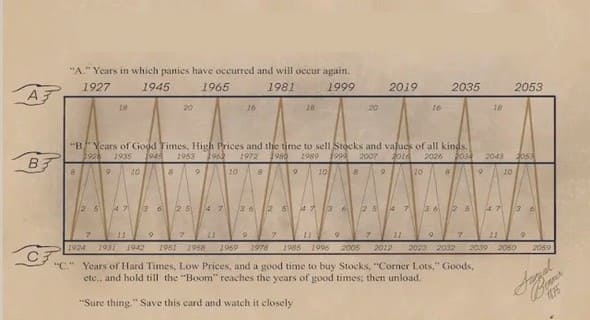
(Downloads - 0)
For more info about our services contact : help@bestpfe.com
Table of contents
Introduction
1 Definitions
1.1 Constraint Satisfaction Problems
1.1.1 Definitions
1.1.2 The satisfiability problem
1.1.3 A graphical representation
1.1.4 More examples of CSP
1.1.5 Other combinatorial optimization problems
1.2 Worst-case complexity
1.2.1 Time complexity
1.2.2 Complexity classes
1.3 An algorithm for the SAT problem
1.3.1 The Unit Clause Propagation procedure
1.3.2 The DPLL algorithm for the SAT problem
1.4 Performances of the algorithms and random CSP ensembles
1.4.1 Complete and incomplete algorithms
1.4.2 Random CSP ensembles
1.4.3 Performances of DPLL on the random k-SAT ensemble
1.4.4 The algorithmic barrier
1.4.5 Some properties of the random hypergraph ensembles
1.5 Statistical physics and constraint satisfaction problems
1.5.1 Boltzmann probability measure
1.5.2 Statistical physics models
1.5.3 Graphical models
2 Phase transitions in random CSPs
2.1 The satisfiability transition
2.1.1 Upper bounds
2.1.2 Lower bounds
2.2 Quenched and annealed averages
2.3 Overview of the phase transitions in random CSPs
2.3.1 The clustering transition
2.3.2 Cluster decomposition
2.3.3 Complexity and the condensation transition
2.3.4 Computing the complexity function
2.3.5 Computing c and sat from the complexity
2.3.6 Rigidity and freezing transitions
2.3.7 Some values of the thresholds
3 Local Search Algorithms
3.1 Simulated Annealing
3.1.1 Monte Carlo method
3.1.2 Metropolis algorithm
3.1.3 Heat bath algorithm
3.1.4 Relaxation time scale of the Monte Carlo dynamics
3.1.5 Cooling scheme
3.2 Focused algorithms
3.2.1 RandomWalkSAT algorithm
3.2.2 WalkSAT algorithm
3.2.3 Focused Metropolis algorithm
4 Message Passing Algorithms
4.1 Belief propagation
4.1.1 BP messages
4.1.2 BP iterations
4.1.3 Marginals
4.1.4 Bethe free entropy and Entropy
4.1.5 Hard-fields
4.1.6 Warning Propagation
4.1.7 Survey Propagation
4.2 Algorithms
4.2.1 Sampling procedure
4.2.2 BP-guided decimation
4.2.3 SP-guided decimation
5 Performance of the algorithms on random Constraint Satisfaction Problems
5.1 Small connectivity k
5.1.1 Two numerical experiments on local search algorithms at small k
5.1.2 Overview of the algorithmic performances for small values of k
5.1.3 Frozen variables and whitening dynamics
5.1.4 Analytical study of the BP-guided decimation
5.2 Large connectivity k
5.2.1 Asymptotic expansion of the thresholds
5.2.2 Algorithmic performances in the large k limit
6 Biased Measures for random Constraint Satisfaction Problems
6.1 Definitions
6.1.1 Biased measure over the set of solutions
6.1.2 Intra-clause bias
6.1.3 Bias with interactions at distance 1
6.1.4 Bias with interactions at larger distance
6.2 Biased measures studied in the literature
6.2.1 Bias counting the frozen variables
6.2.2 Local entropy
6.2.3 Biased interactions in the hard sphere packing problem
7 Cavity Method
7.1 Definition of the model
7.1.1 Graphical model
7.1.2 BP equations and Bethe free-energy
7.2 Replica symmetric cavity method
7.2.1 RS cavity equations
7.2.2 Intra-clause bias
7.2.3 Bias with interaction at distance 1
7.3 The dynamic transition
7.3.1 The broadcast process
7.3.2 The reconstruction problem and its recursive distributional equations
7.4 Hard fields and the naive reconstruction
7.4.1 Intra-clause bias
7.4.2 Bias with interactions at distance 1
7.5 The distribution of soft-fields
7.5.1 Uniform measure
7.5.2 Bias with interaction at distance 1
7.6 1RSB formalism
7.6.1 1RSB cavity equations
7.6.2 Simplifications for X = 1
7.6.3 Complexity (X = 1) and condensation threshold
7.7 Kesten-Stigum bound
7.7.1 Intra-clause bias
7.7.2 Bias with interactions at distance 1
8 Finite k results
8.1 Numerical resolution for finite k
8.2 On the numerical determination of the dynamic transition
8.2.1 Scalar bifurcations
8.2.2 Discontinuous functional bifurcations
8.2.3 The stability parameter in the functional case
8.3 Results of the cavity method
8.3.1 The existence of a RS phase for > d,u
8.3.2 More detailed zero temperature phase diagrams
8.4 Results of Simulated Annealing
8.4.1 Estimating the algorithmic threshold for Simulated Annealing
8.4.2 Performances of Simulated Annealing with optimal RS parameters
8.4.3 Performances of Simulated Annealing with the biased measure
8.5 Comparison with the biased measure with interactions at distance
9 The asymptotics of the clustering transition for the uniform measure
9.1 The large k limit for a finite distance n
9.1.1 Evolution of the hard fields
9.1.2 The reduced order parameter
9.1.3 Evolution of the soft fields distribution
9.2 The limit of large distance n
9.2.1 The regime
9.2.2 The difficulties for < 1
9.2.3 Reweighted probability distributions
9.2.4 Numerical resolution
9.2.5 The fixed point equation and the determination of d
9.2.6 An analytic lower bound on d
10 The asymptotics of the clustering transition for biased measures
10.1 A first upper-bound for the intra-clause bias
10.2 The asymptotics of the clustering threshold
10.2.1 Setting
10.2.2 A specialization of some formulas
10.3 The large k limit for a finite distance n
10.3.1 Evolution of the hard fields
10.3.2 Evolution of the soft fields distribution
10.4 The limit of large distance n
10.4.2 A reweighting scheme
10.4.3 A Gaussian approximation for the quasi-hard fields
10.4.4 Algorithmic implementation
10.5 Results
Conclusion
Bibliography