Get Complete Project Material File(s) Now! »
Chapter 4 Analysis of Digital Relay Implementation
Introduction
In the previous chapter a testing platform was designed and implemented in the form of a digital relay. This chapter will use that testing platform in conjuction with the results from Chapter 2 to critically assess and compare the performance of the phasor estimation algorithms in three parts. The rst part assesses the computational requirements and e ciency of the proposed algorithm for phasor estimation using the Discrete Wavelet Transform. The second part then compares the accuracy and performance of the proposed algorithm with the phasor estimation using the Discrete Fourier Transform algorithm using fault waveforms generated in simulations of the distribution feeder as detailed in Chapter 2. The third part compares the phasor estimation algorithms using speci c, mathematically generated signals to assess their performance with speci c signal components and characteristics that are expected to be present in the signal from a CT/VT during a fault.
Algorithm Analysis Breakdown of DWT Phasor Estimation Algorithm
In analysing the parts of the DWT phasor estimation algorithm it was determined that the largest single portion is spent calculating values for the synchronized reference waveform (3.24), a huge 36% as shown in Figure 4.1. This could be reduced considerably by generating a lookup table of the waveform and then ‘shifting’ the wave so its phase matches the sampled waveform phase. This disadvantage of this would be reduced accuracy when calculating the magnitude as the shifted waveform may not be a close enough match to the phase and also there would be increased program memory use. However if this was implemented, the only computational time required for this portion would be to move values from one location in memory to another, so the computational time required for the DWT phasor estimation would be 64% of the current time, so in the case of the Daubechies 8, 1 level, full cycle algorithm in Figure 4.3, this would be 17.5 s, instead of the current 27.4 s, putting it in the same category as performing a 256 point FFT. The next largest parts are the two DWT’s with 17% each, these are currently implemented using the lter method as described in (3.28). They may be able to be optimized further by using the lifting method as described in [36], but this would remove the exibility of being able to implement di erent wavelets. Since this and most other DSPs have optimized instructions for lter coe cient calculation it was not implemented in this case.
Comparing the DWT with the FFT computation time
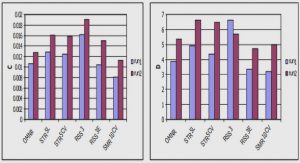
Figure 4.2 compares the computation time required for phasor estimation using the Discrete Wavelet Transform with the computation time required for phasor estimation with the Discrete Fourier Transform (implemented using the Fast Fourier Transform algorithm). The wavelets Haar, Daubechies 4, Daubechies 8 and Daubechies 10 are tested with varying sizes of the Fast Fourier Transform. In terms of computational time phasor estimation using the Discrete Wavelet Transform does not require much more processing power, and depending on which size FFT is used may even require less such as in the case of the 512 point (or larger) FFT.
Comparing execution time of wavelets
Four di erent wavelets were tested and implemented using the DWT phasor estimation algorithm, their execution time is compared in Figure 4.3. The di erence in execu-tion time is small, with full cycle analysis the variation between Haar (special case of Daubechies 2) and Daubechies 10 is only 17%, and with with half cycle analysis this becomes 28%. This may become more of an issue if the total computation time can be reduced by the method suggested in the DWT phasor estimation algorithm break-down. As the computation time is under 30 s real time processing can be performed at sampling rates of up to 11kHz when using this processor to calculate all three phases.
Comparing execution time of di erent levels of decomposition of DWT
Recursion was also implemented to add extra levels of decomposition of the DWT to add further ltering as detailed in Section 3.4.4. As shown in Figure 4.4 recursion does not add a signi cant ammount of extra processing time when using the DWT algorithm. This is because the only extra processing required is of the DWT itself, which is shown from the analysis of the algorithm in Section 4.2.1 to only contribute to 11% of the total processing time.
Relay Test Bench Setup
For realtime testing of the phasor estimation algorithms in the implemented digital relay a lab test bench was assembled as shown in Figure 4.5. A block diagram of this system is shown in Figure 4.6 and is described below. A standard IEEE 13 bus distribution feeder is simulated in PSCAD (as described in Chapter 2) and the current waveforms as would be seen by a CT and overcurrent relay located as they would be in an actual feeder are generated. They are captured and stored in the industry standard IEEE COMTRADE [37] le format. The COMTRADE le format was chosen as it is the le format used by fault recorders and other protection devices to capture fault waveforms on electricity networks and was designed speci cally for this purpose. This will also allow an opportunity for future research to test the performance of relay algorithms using fault signals captured directly during faults on electricity networks. LabView [38] based software developed for numerical testing of digital relays as a 2009 Honours project [39] is used to load the COMTRADE les, then generate the analogue waveforms using a National Instruments NI 9263 Analog Output Module .The implemented Digital Relay samples the waveform using its analogue to digital converter. The sampled waveform is then processed by the algorithms under test to estimate the current phasors. The estimated current phasors are then communicated back from the DSP to the PC for analysis using the JTAG interface.
Results of testing with simulated waveforms
The rst test performed was the case of the double line to ground fault (phases A and from Figure 3 in Section 2.5.2.1. This was chosen as it presented the worst case of likely faults with the highest level of decaying DC o set in the IEEE 13 bus feeder. The result of this using the full cycle implementation is shown in Figure 4.7 and from this we can see that Discrete Fourier Transform is able to estimate the phasor accurately, with the phasor estimation using the Discrete Wavelet Transform overshooting by a factor of 12% due to the decaying DC o set present at the moment of the fault. As this is a full cycle implementation the DFT is able to remove the majority of the decaying DC. It was also observed from this test that some high frequency noise remains in the signal with a small oscillation occurring throughout the time period showing that more ltering may be required. The result of this using the half cycle implementation is shown in Figure 4.8 and shows that with the harmonics and decaying DC o set present in the waveform neither the DFT nor the DWT can estimate the phasor accurately from the raw waveform, both oscillate signi cantly around the value. To attempt to remove the high frequency oscillations present in the estimated phasors a higher decomposition level was used for the DWT, the result of which is shown in Figure 4.9. It shows that the higher level of decomposition had no signi cant e ect on the oscillations, but it did introduce a larger error in the phasor estimation. When calibrating the test setup, speci cally the 0.0 Volt point it was also noted that any DC o set at all caused signi cant errors in the phasor estimation when using the DWT, whereas the DFT was able to ltering out any constant DC o set. This meant the DFT e ectively required no calibration for the 0.0 Volts point, whereas the DWT would need to be carefully calibrated and the calibration would need to be maintained, or the signal would need to be pre- ltered to remove any DC o set.
1 Introduction
1.1 Background Study
1.2 Research Motivation
1.3 Aims and Objectives
1.4 Scope of the Thesis
1.5 Publications
2 The Emerging Distribution Network
2.1 Introduction
2.2 Current Distribution Network
2.3 Protection Devices in a Distribution Network
2.4 Future Developments
2.5 Simulations
2.6 Discussion
3 Implementation of Digital Relay
3.1 Introduction
3.2 Phasor Estimation
3.3 Hardware
3.4 Software
4 Analysis of Digital Relay Implementation
4.1 Introduction
4.2 Algorithm Analysis
4.3 Relay Test Bench Setup
4.4 Comparison of the DWT and DFT in the Implemented Digital Relay
GET THE COMPLETE PROJECT
Adaptive Protection for Smart Grids