La modélisation du séchage et du transfert de gaz

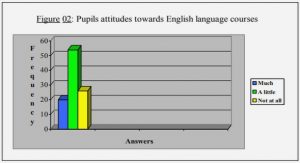
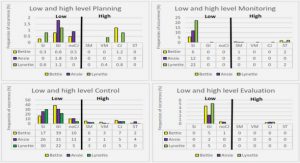
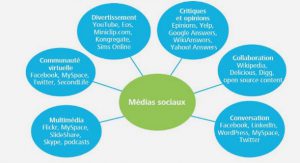
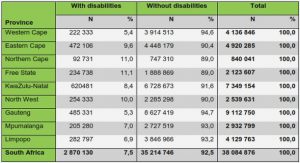
Get Complete Project Material File(s) Now! »

Data and Measurement System

IFLS Data

My main source of outcome variable data is the Indonesia Family Life Survey (IFLS) (RAND, 1994, 1997, 2000, 2008, 2015). This is a comprehensive longitudinal survey with 5 waves between 1993 and 2015 that contains detailed information on over 30,000 individuals. These individuals come from 13 of the 27 provinces in the country and are representative of approximately 83% of the Indonesian population. A wide range of questions are asked to each respondent, covering multiple areas of socioeconomic and human capital status. Particularly relevant to this paper, later waves include multiple questions on cognitive ability and other socio-emotional dimensions including mental health, subjective wellbeing, personality, positive and negative affect, and risk and time preferences. Cognitive questions include versions of Raven’s progressive matrices (John and Raven, 2003) and number series tests, some of the most widely used measures in the literature. Subjective wellbeing and emotional “affect” are measured using cognitive evaluation questions such as the Cantrill Ladder, along with questions relating to positive and negative emotions the respondent felt in the last day. Personality questions are based on the “Big 5” personality traits (Rammstedt and John, 2007), and the mental health questions are based on the CES-D depression scale (Radloff, 1977). Both of these are extensively used in the psychology and economics literature. More details on the individual measures are found in Appendix Section A.1. In order to combine measures of traits into low-dimensional factors, I use a latent factor model in the style of (Heckman et al., 2013) to generate factor scores that are then used as the dependent variables in my main specification. This process is described further in Section 3.3 and in Appendix Section B.
10Skills are naturally assumed to be a positive function of investment, so dmk/dg > 0 and ¶g/¶I2 > 0.
The IFLS data include the measurements of height and weight that I use for results on anthropometrics, and measures of household consumption that I use to construct an overall measure of household expenditure. It further includes the multiple other demographic and socioeconomic variables that I use as controls in my models, such as gender, religion, and education levels. I also make use of detailed information on pregnancy history, child investment, and other behaviours of parents and children during individuals’ early life to create the variables used in the mediation analysis.
The survey contains detailed information on an individual’s location at birth and, for individuals older than 15, a full migration history tracking an individual’s location at age 12 and every migration thereafter. I am able to combine this retrospective data with the contemporaneous data on location of respondents at each of the five IFLS waves (in 1993, 1997, 2000, 2007, and 2015) to construct a year-by-year history of each individual’s location. I also use information on whether the individual was born in a rural household to restrict to only the rural population, under the assumption that these are the households for whom weather shocks are likely to have a significant effect on household welfare through changes in agricultural income.
More detail on the measures used in the IFLS data can be found in Section A.1 in the Appendix.

District, Weather, and Crop Data

The primary weather variable I use in the paper is the Standardised Precipitation Evapotranspiration Index (SPEI), a drought index developed by Vicente-Serrano et al. (2010). Although most of the economic literature on weather shocks focuses solely on precipitation or temperature, this neglects other features of the climate that can affect the growing cycle of a plant. In particular, the impact of rainfall on crop cycles depends on potential evapotranspiration (the ability of soil to retain water), which is in turn affected by multiple features of the environment, including temperature, latitude, windspeed, and the number of sunlight hours. SPEI is a rich index that combines all of these features. It has been shown to be a better predictor of crop yields and other ecological and hydrological variables than other climate indexes in a variety of climactic contexts Beguer´ıa et al. (2014).
I use monthly gridded data for SPEI from the Global SPEI database that is available in grids of 0.5 latitude by 0.5 longitude (approximately 50km by 50km at the equator) (Beguer´ıa and Vicente Serrano, 2017). The SPEI is a standardised index, so that a value of 1 represents weather conditions that are 1 standard deviation higher on the SPEI scale compared to the local historical average (1900-2015). I use GIS shapefile data on Indonesian districts to match each district to its overlapping grids and calculate district-level SPEI by taking a weighted average of these overlapping grids.
This monthly district SPEI is used to construct the main SPEIi(t+j) variable used throughout the paper by calculating the average district SPEI over the growing season of the main crop of that district in that period. For the main specification, I match this shock back to individuals using the constructed year-by-year record of each individual’s location described above. For example, the variable SPEIi(t+2) for an individual i born in t would denote the average SPEI during the growing season of the main crop of the district where i spent the year of her life after her 2nd birthday.
I describe this process in more detail, along with the relevant sources for each dataset, in Appendix Section A.2.

Measurement of skills

The use of the psychological outcome measures seen in the IFLS as outcome variables presents at least two key empirical challenges. First, psychological measures tend to be “riddled with measurement error” (Cunha and Heckman, 2009; Heckman et al., 2013). If such error is classical, it may lead to imprecise estimates of causal effects. If it is non-classical, then it may bias the estimated impact of weather shocks on psychological outcome variables. Moreover, such error may be even more severe in low- and middle-income country contexts (Laajaj and Macours, 2017; Laajaj et al., 2018). Second, each psychological measure doesn’t truly represent an independent variable. For example, the responses to two questions such as (i) “I see myself as someone who is outgoing and sociable” and (ii) “I see myself as someone who is talkative” are likely to be two proxy measures of a single psychological trait, in this case extraversion. We therefore require a method of condensing highly intercorrelated measures down to a lower-dimensional set of psychological skills.
In this paper I use the latent factor model seen in Cunha et al. (2010) to combine psychological measures.11 This technique is commonly used in the psychometric literature, and it partially deals with the two problems described above by explicitly accounting for random (but not systematic) measurement error and by reducing observed measures down to a lower-dimensional set of latent factors. Suppose, for example, that for each individual i there are three different survey questions that relate to extraversion fYi1, Yi2, Yi3g. The latent factor model assumes that these all measure the underlying factor Fi (e.g. extraversion) along with some measurement error fu1i, u2i, u3ig.
We can then use a process of exploratory factor analysis to recover the latent factor score Fi from each of the measures fYi1, Yi2, Yi3g, for example by using maximum likelihood estimation to fit the model.
The process and results used to generate factor scores is described in detail in Appendix Section B, and the results are summarised in Table 1. Running a factor analysis exercise on cognitive measures suggests that there is a single cognitive factor that is proxied by all the cognitive measures available in the data. Running a separate factor analyis exercise on socioemotional measures indicates that there are 3 latent factors being measured. The measures in each of the 3 latent factors align relatively closely with the survey module structure, meaning that each has an easily applicable interpretation (based on the measures from which it is composed)12. The first I interpret as “affect / wellbeing”. This is mostly composed of measures from the Positive-Negative Affect module of the IFLS survey, which asks about which emotions the individual felt in the past week, and also includes standard life-evaluation questions such as the Cantrill Ladder. The second factor I interpret as “personality”, and is composed of questions from the Big 5 personality test. The interpretation of this factor is somewhat less clear as it mixes questions which are meant to identify distinct personality traits such as extraversion and conscientiousness.13 The third factor is exclusively composed of questions from the CES-D depression scale, and so can be clearly interpreted as “mental-health”. A fuller discussion of the interpretation of each factor is found in Appendix Section B. Having generated the factors from the psychological measures, I then have factor scores for each individual which are used as dependent variables in the main results of the paper. Note that these factors are always to be interpreted “positively” (in line with previous literature which sees these traits as skills, see e.g. Cunha et al., 2010). For example, a higher mental health factor score will mean better mental health or less depression. Moreover, the scores are normalised to have a mean of 0 and a standard deviation of 1 so that they can be easily interpreted. For example, a mental health factor score of 1 can be interpreted as saying that the individual’s mental health is one standard deviation above the sample average.

Samples and summary statistics

In order to make full use of the wealth of the IFLS data in order to understand both the effects of weather shocks and the mechanisms through which they can affect adult psychological outcomes, I run analyses on a number of different samples with different units of observation. For clarity, these samples are summarised in 2. All samples are restricted to rural only, under the assumption that urban households are unlikely to be affected by weather shocks, while rural households are likely to be impacted by these shocks through changes in agricultural incomes. The “main sample” used in Sections 5.1 and 5.2 includes all the individuals born after 1988 in the IFLS data for whom there is either socio-emotional or cognitive outcome data available. Since the first wave of the IFLS data was in 1993, focusing on individuals born after 1988 means that I will have some data available on individuals during their childhood (such as measures of early life investment in the child), which can then be used in a mediation analysis.14 15 The mediation samples (one for each mediator) are the subsets of the main sample that have non-missing values for the relevant mediator (see more discussion in Section 6.3.1 on the methodology for mediation analysis). Both the main and the mediation samples are at the level of the individual.16 For the results on household expenditure (Section 6.1), I do not restrict to households containing individuals in the main sample but instead use all available rural households in the IFLS data. I also use a repeated cross-sectional specification in which one observation is a (household wave). For the results on anthropometrics (Section 6.2) I also do not restrict to the main sample, and instead increase sample size by using all individuals who were measured at least once between the ages of 0 and 5 years old in rural households17. This sample is also treated as a repeated cross-section where one observation is (individual wave).
Table 3 presents summary statistics for individuals in the main sample. As noted above, the factor scores for each of the psychological variables is normalised so that by construction, the mean is 0 and the standard deviation is 1. Note that since Affect/Wellbeing and Personality were only measured in the 5th wave of IFLS (in 2015), any members interviewed only in IFLS4 (in 2007) have missing values for these variables. Therefore N is only 4672 for these factors.18 Roughly half of the sample (47%) were born during the growing season of the main crop in their district. The main weather shock variables used in Results section 5.1 and 5.2 are the SPEI growing season from t 2 to t + 15 (denoting the weather conditions 2 years before birth up to 15 years after birth). Since the SPEI is a standardised index we expect the mean to be approximately 0. As we can see, the mean of SPEI growing season is above 0 for all years after birth, suggesting that on average, the weather conditions experienced by members of the main sample after birth were slightly more favourable than the historical average from 1900 to 2015. The standard deviation for each SPEI shock variable is consistently between 0.43 and 0.46, suggesting substantial variation between individuals in the weather conditions experienced at every age. As noted above, the main sample is restricted to only include individuals born after 1988 and the median individual is born in 1992. 54% of the main sample are female. The vast majority of the sample (90%) are Muslim while 5% are Hindu, 4% Protestant, and 1% some other religion. The highest level of education reached by a parent of sample members is typically elementary (52%), while 19% have a parent that reached Junior High School, 20% have a parent that reached Senior High, and 8% have a parent that reached university.

Empirical Strategy

To test for the effect of early-life weather shocks on adult psychological outcomes, I estimate the following equation: J=15 Yirt = a + å bjSPEIi(t+j) + pGir + Xi0g + dr + mt + #irt j= 2
Here, Yirt denotes the adult psychological outcome variable of interest for an individual i born in region r at time t.19 In Section 5.1, I use the factor score for cognitive skills, while in Section 5.2 I use the three socio-emotional factor measures: affect/wellbeing, personality, and mental health. My weather shock variable is SPEIi(t+j). This is a shock variable based on the SPEI climate indicator as described in Section 3, and matched back to individuals so that SPEIi(t+j) describes the average SPEI over the growing season of the main crop in the district where i was located in the year after their jth birthday, according to the constructed location history I described in Section 3.1.20 Gi is an indicator variable that takes the value 1 when the individual i was born during the growing season of their birth district r. Xi is a vector of individual-level controls, that (in the preferred specification) includes dummies for the highest level of education achieved by a parent of i, dummies for religion, and a female dummy. dr and mt are birth-region and birth-year fixed effects, while a denotes the intercept.
The coefficients of interest in this specification are bj, j 2 f 2, 1, …, 15g. These allow me to test for the effects of weather shocks at different stages of life on adult psychological outcomes. In particular, I can look at the different effects of weather conditions before birth (j 2 f 2, 1g), at birth (j = 0), in early childhood (j 2 f1, …, 5g) and later childhood (j 2 f6, …, 15g). The key advantage of my empirical setting when trying to make such distinctions is that weather shocks are unlikely to be serially correlated over multiple years.21 To illustrate, the empirical correlation in the main sample between SPEIi(t+s) and SPEIi(t+s 1) (that is, the correlation between a shock and the 1 period lag) is only 0.076 (95% confidence interval: [0.071, 0.081]). This means that the weather shocks provide significant variation that is independent year on year and allows me to make fine-grained distinctions between effects in each year.
The birth-year fixed effects control for any unobserved factors that are common to all individuals in the sample born in the same year, such as macroeconomic shocks. The birth-region fixed effects control for any time-invariant unobserved factors that are common across all individuals born in the same region. My identification strategy then relies on the claim that conditional on these birth-year and birth-region fixed effects, the SPEI shocks are exogenous.
One notable threat to this identification strategy would be if there are endogenous reactions to weather shocks that confound the causal effect of weather shocks on adult psychology. Suppose, for example, that some families are able to migrate within a given year to areas with favourable weather, and families of higher cognitive ability are more likely to do so. In this case the positive correlation between SPEIi(t+j) and adult cognitive ability would confound the causal effect of a shock with this selection effect. This seems unlikely; although migration is common in the sample, it is implausible that rural households are able to react sufficiently quickly to seasonal weather patterns. Another possibility is selective mortality. For example, if extreme negative weather shocks (such as drought) lead to the death of children, and these deaths are concentrated upon those children who would otherwise have developed poorly, then any positive relationship between weather shocks and adult psychological outcomes would be biased downwards. I test for such an effect in Appendix Section D, and show that while there may be a positive impact of SPEI shocks in utero on infant mortality, the magnitude is small and appears not to affect the probability of inclusion in my main sample. This implies that selection bias will be close to 0, although it cannot be ruled out entirely. Absent such selection bias, the coefficients on bj will be unbiased estimates of the impact of early-life weather shocks on adult psychology.

Table of contents :

INTRODUCTION GENERALE
1. Problématique :
1.1 Présentation du contexte industriel
1.2 L’énergie Nucléaire en France
1.3 La conception et réglementation des centrales nucléaires françaises
2. Objectif de l’étude
PARTIE A : ETUDE BIBLIOGRAPHIQUE
1. Généralité sur les bétons
1.1 Pâte de ciment
1.1.1 Les hydrates
1.1.2 La porosité
1.2 Granulat
1.2.1 Les granulats naturels
1.2.2 Les granulats artificiels
1.2.3 Les granulats recyclés
1.2.4 Auréole de transition
1.3 Adjuvants et additions
2. Le séchage des bétons
2.1 Mécanismes du séchage et caractérisation expérimentale
2.1.1 Les mécanismes du séchage
2.1.2 Caractérisation expérimentale du séchage
2.2 Les effets du séchage
2.2.1 Effet sur les propriétés mécaniques
2.2.2 Effet du séchage sur le transfert de gaz
2.3 La modélisation du séchage et du transfert de gaz
2.3.1 Equations de conservation de la masse : approches complètes
2.3.2 Equations de conservation de la masse : approche simplifiée pour le séchage
2.3.2.1 Equations constitutives
2.3.2.2 Identification des paramètres de séchage
2.3.3 Autre approche pour la modélisation du séchage
2.3.4 Equations de conservation de la masse : approche simplifiée pour le transfert de gaz
2.3.4.1 Conditions aux limites pour le séchage
2.4 Conclusion
3. La fissuration des bétons
3.1 Observations expérimentales de la fissuration
3.1.1 Comportement en compression uniaxiale
3.1.2 Comportement en traction uniaxiale
3.1.3 Modélisation de la fissuration
4. Les déformations différées dans le béton
4.1 La déformation de retrait de dessiccation
4.1.1 Caractéristiques du retrait de dessiccation
4.1.1.1 Effet structural du retrait de dessiccation
4.1.1.2 Effet de la composition du matériau sur le retrait de dessiccation
4.1.1.3 Effet de la fissuration induite par le retrait sur le séchage
4.1.2 Les mécanismes du retrait de dessiccation
4.1.3 Modélisation du retrait de dessiccation
4.1.3.1 Modélisation phénoménologique
4.1.3.2 Modélisation basée sur la mécanique des milieux poreux
4.2 Etude des déformations de fluage propre
4.2.1 Observations expérimentale
4.2.1.1 Le fluage propre en compression
4.2.1.2 Le fluage propre en traction directe
4.2.1.3 Fluage propre en flexion trois points
4.2.1.4 Comparaison des courbes de fluages spécifiques en traction et en compression
4.2.2 Les mécanismes de fluage propre
4.2.2.1 Mécanisme à court terme
4.2.2.2 Mécanisme à long terme
4.2.3 Modélisation du fluage propre
4.2.3.1 Cadre de la viscoélasticité linéaire
4.2.3.2 Couplage fluage/fissuration
4.3 Etude des déformations de fluage de dessiccation
4.3.1 Observations expérimentales
4.3.1.1 Le fluage de dessiccation en compression
4.3.1.2 Le fluage de dessiccation en traction
4.3.1.3 Comparaison des courbes de fluage spécifique en compression et traction
4.3.2 Les mécanismes de fluage de dessiccation
4.3.3 La modélisation du fluage de dessiccation intrinsèque
4.4 Montages expérimentaux pour la caractérisation du fluage
4.4.1 Etude du fluage en traction au jeune âge par déformation empêchée ou gênée
4.4.2 Essai à l’anneau
4.4.3 Dispositif de traction directe
5. Conclusion
PARTIE B : ETUDE EXPERIMENTALE
1. Composition, mise en oeuvre et conservation du matériau
1.1 Composition du matériau étudié
1.1.1 Références sur le B11
1.1.2 Nature des constituants de notre étude
1.1.2.1 Les granulats
1.1.2.2 Le ciment
1.1.3 Formulation
1.2 Mise en oeuvre et conservation du matériau
1.2.1 Fabrication
1.2.2 Essai de surveillance de la prise du béton grâce aux ultrasons
1.2.3 Cure du matériau
2. Présentation des différentes campagnes expérimentales
2.1 Campagne expérimentale du fluage en traction uniaxiale (LCPC)
2.1.1 Bâti de fluage en traction directe
2.1.2 Etalonnage des masses
2.1.3 Description des éprouvettes
2.1.4 Instrumentation des essais
2.1.4.1 Eprouvette 13×50 cm
2.1.4.2 Eprouvette 16×100 cm
2.1.5 Collage et décollage des éprouvettes
2.1.5.1 Collage
2.1.5.2 Décollage
2.1.5.3 Caractérisation mécanique de la colle
2.1.6 Conditions d’essais pour la mesure des déformations différées (LCPC)
2.1.7 Acquisition des données
2.1.8 Mesure de débit
2.2 Tests préliminaires
2.2.1 Détermination de la résistance en traction
2.2.2 Essais de fluage avec mesure de débit d’air
2.3 Campagne de fluage en traction avec pré-séchage des éprouvettes
2.4 Campagne expérimentale du fluage en compression (LMT)
2.4.1 Bâtis de fluage en compression
2.4.2 Description des éprouvettes
2.4.3 Positionnement des éprouvettes sur le bâti
2.4.4 Instrumentation des essais
2.4.5 Conditions d’essais pour la mesure des déformations différées (LMT)
3. Présentation des essais
3.1 Décomposition des déformations de fluage
3.2 Campagne de fluage en traction
3.2.1 Protocole expérimental
3.2.2 Présentation des différents essais (LCPC)
3.2.3 Cycle de vie d’une éprouvette
3.3 Campagne de fluage en traction avec préséchage
3.3.1 Présentation des différents essais (préséchage)
3.3.2 Mesure de débit
3.3.3 Niveau de chargement
3.4 Campagne de fluage en compression
3.4.1 Présentation des différents essais (LMT)
4. Conclusion
PARTIE C : RESULTATS ET ENSEIGNEMENTS
1. Présentation et analyse des résultats
1.1 Caractéristiques mécaniques du B11
1.2 Evolution de l’ambiance
1.3 Séchage
1.3.1 Perte en masse
1.3.1.1 Perte en masse LCPC (20°C, 50 % HR)
1.3.1.2 Perte en masse LMT (19°C, 42 % HR)
1.3.1.3 Perte en masse LMT (25°C, 60 % HR)
1.3.1.4 Perte en masse à 40°C et 80 % HR
1.3.1.5 Comparaison des suivis de perte en masse
1.3.2 Isotherme de désorption
1.3.3 Porosité
1.4 Déformations de retrait de dessiccation
1.4.1 Suivi des déformations d’origine thermique [LCPC]
1.4.2 Evolution du retrait de dessiccation en fonction du temps
1.4.2.1 Essais LCPC (20°C et 50% HR)
1.4.2.2 Essais LMT (19°C et 42 % HR)
1.4.2.3 Essai de retrait de dessiccation à 20°C, 50 % HR avec préséchage à 40°C et 80 % HR 15
1.4.2.4 Comparaison des déformations de retrait de dessiccation en fonction du temps
1.4.3 Détermination du retrait de dessiccation en fonction de la perte en masse
1.4.3.1 Essais LCPC (20°C et 50% HR)
1.4.3.2 Comparaison des résultats de retrait de dessiccation en fonction de la perte en masse
1.5 Essai de fluage propre
1.5.1 Fluage propre en traction
1.5.1.1 Essais de fluage propre LCPC
1.5.1.2 Comparaison des courbes de fluage propre spécifique en traction
1.5.1.3 Essais de fluage propre en traction avec préséchage
1.5.2 Fluage propre en compression
1.5.2.1 Essais de fluage propre LMT
1.5.2.2 Comparaison des essais de fluage en compression
1.5.3 Comparaison des courbes de fluage propre spécifique en traction et en compression
1.6 Fluage de dessiccation
1.6.1 Fluage de dessiccation en traction
1.6.1.1 Essais de fluage de dessiccation LCPC
1.6.1.2 Comparaison des courbes de fluage de dessiccation spécifique en traction
1.6.1.3 Essais de fluage de dessiccation avec préséchage
1.6.2 Fluage de dessiccation en compression
1.6.2.1 Essais de fluage de dessiccation LMT
1.6.3 Comparaison des courbes de fluage de dessiccation spécifique en traction et en compression
1.6.4 Comparaison entre le fluage de dessiccation et le fluage propre
1.6.5 Proportionnalité entre le fluage de dessiccation et le retrait de dessiccation
1.7 Propriétés mécaniques résiduelles
1.7.1 Evolution du module d’Young
1.7.2 Effet du séchage sur la résistance du béton (sans fluage)
1.7.3 Incidence du fluage et du séchage sur la résistance en traction résiduelle
1.7.4 Incidence du fluage et du séchage sur la résistance en compression résiduelle
1.7.5 Comparaison de la résistance résiduelle en compression et en traction
1.8 Conclusion
2. Simulation numérique des résultats
2.1 Modélisation du séchage
2.1.1 Description du modèle
2.1.1.1 Equation de conservation de la masse
2.1.1.2 Conditions aux limites en surface
2.1.1.3 Validation de l’approche simplifiée pour décrire le séchage
2.1.2 Identification des paramètres matériaux
2.1.2.1 Porosité
2.1.2.2 Isotherme de désorption
2.1.3 Simulation numérique du séchage sans prise en compte de la convection
2.1.3.1 Suivi de la perte en masse LMT (25°C et 60% HR)
2.1.3.2 Influence des conditions aux limites pour l’essai LCPC (20°C et 50% HR)
2.1.3.3 Influence de l’humidité relative interne initiale de l’éprouvette
2.1.3.4 Identification de la perméabilité intrinsèque pour les différentes courbes de perte en masse
2.1.3.5 Suivi de la perte en masse LMT en enceinte climatique (19°C, et 42% HR)
2.1.3.6 Suivi de la perte en masse LCPC (20°C, et 50% HR)
2.1.3.7 Récapitulatif des paramètres identifiés
2.1.4 Simulation numérique du séchage avec prise en compte de la convection
2.1.4.1 Simulation des essais LCPC (20°C et 50% HR)
2.1.4.2 Simulation des essais LMT (19°C et 42 % HR)
2.1.4.3 Simulation des essais LMT (25°C et 60 % HR)
2.1.4.4 Bilan des différentes simulations numériques (sans préséchage)
2.1.4.5 Simulation des essais de préséchage (40°C et 80 % HR)
2.1.4.6 Simulation des essais (20°C et 50 % HR) après préséchage (40°C et 80 % HR)
2.1.4.7 Récapitulatif des paramètres identifiés (avec convection)
2.1.5 Conclusion
2.2 Modélisation de la fissuration
2.3 Modélisation du retrait de dessiccation
2.3.1 Simulation des essais de retrait de dessiccation (séchage sans convection)
2.3.2 Simulation des essais de retrait de dessiccation (séchage avec convection sans prise en compte du fluage)
2.3.2.1 Simulation des essais de retrait de dessiccation LCPC (20°C et 50% HR)
2.3.2.2 Simulation des essais de retrait de dessiccation LMT (19°C, 42 % HR)
2.3.2.3 Simulation des essais de retrait de dessiccation LCPC 2008 (20°C, 50 % HR)
2.3.2.4 Simulation des essais de retrait de dessiccation (20°C, 50 % HR) avec préséchage (40°C, 80 % HR)
2.3.2.5 Bilan de l’identification des paramètres matériaux
2.3.3 Conclusion
2.4 Modélisation des déformations de fluage propre
2.4.1 Description du modèle utilisé
2.4.2 Identification des paramètres matériaux
2.4.3 Conditions aux limites
2.4.4 Simulation du fluage propre en traction
2.4.5 Simulation du fluage propre en compression
2.4.6 Modélisation combinée du fluage propre en traction et en compression
2.4.7 Conclusion
2.5 Modélisation des déformations de fluage de dessiccation
2.5.1 Conditions aux limites
2.5.2 Analyse des déformations de fluage de dessiccation
2.5.2.1 Essais LCPC en traction (20°C, 50 % HR)
2.5.2.2 Réanalyse du retrait de dessiccation avec prise en compte du fluage (20°C, 50 % HR)
2.5.2.3 Essais LMT en compression (19°C, 42 % HR)
2.5.2.4 Essais LCPC 2008 en traction (20°C, 50 % HR)
2.5.3 Conclusion
2.6 Etude de l’interaction entre la fissuration et les déformations de fluage propre et dessiccation
2.6.1 Modélisation du couplage fluage fissuration
2.6.2 Identification du paramètre de couplage
2.6.3 Rupture pendant l’essai de fluage en traction (essais LCPC)
2.6.3.1 Cas du fluage propre
2.6.3.2 Cas du fluage de dessiccation
2.6.3.3 Conclusion
2.7 Conclusion
CONCLUSION GENERALE
REFERENCES BIBLIOGRAPHIQUES
ANNEXES

GET THE COMPLETE PROJECT